Mastering Plastic Design: Efficient Strain-Based Methods for Reliable Components

This article deals with the following topics:

• IMT’s innovative approach to strain-related design enhances the performance and reliability of plastic components.
• Strain-based design provides a more appropriate assessment of plastic behavior compared to conventional stress-based methods.
• Accurate evaluations of short-term and long-term material behavior, even without extensive material data.
• Combines advanced simulations, literature values, and pragmatic estimation methods.
• Ensures fast and cost-effective development processes for complex applications.

 

Introduction

Plastic components play a vital role in modern device development for various industries such as medical and consumer electronics. Their advantages include lightweight properties, cost-effectiveness, and versatile design possibilities. However, designing plastic parts also presents unique challenges due to their dependency on temperature, aging effects, and the diversity of material formulations and blends. Furthermore, limited material data, especially regarding temperature dependencies and long-term behavior, can complicate the design process. These challenges necessitate a specialized yet efficient approach to ensure plastic components maintain performance and safety over their expected lifespan while keeping the development process fast and cost-effective.

IMT’s approach aims to provide accurate and pragmatic assessments of both short-term and long-term behaviors of plastic components. The goal is to take into consideration the unique properties of plastic materials by using strain to quantify their behavior under load. Further, using literature values and approximation methods developed in academia allows to assess material behavior even before having extensive material properties from long-term tests at hand.

Efficient Strain-Based Methods

Unlike conventional stress-based methods, strain-based design offers a more realistic evaluation of plastic behavior under load, accommodating the viscoelastic nature of plastics and enabling reliable predictions of material performance under complex conditions. The basic assumption underlying the strain-based evaluation of plastic components is that failure occurs at a strain value that is independent of the corresponding stress [1]. This can be formulated as deformation condition [2]:

\( ε_{max} = max⁡(ε_1,ε_2,ε_3 ) ≤ ε_{permissible} = ε_G * \frac{C_1 * C_2 * … * C_n}{S} \)

Where \( ε_1,ε_2,ε_3 \) are the principal strains in the material, \( ε_G \) is the strain limit, \( C_i \) are influencing factors and \( S \) is a safety factor. More information regarding these quantities will be given in the following sections.

 

Strain limit \( ε_G \)

Central to IMT’s method is the concept of "reversibility strain" and its limit value, which facilitates dimensioning of plastic components. The basic idea builds on the concept of a “reversibility strain” \( ε_F (t,ϑ,…) \) which is dependent on duration of the load \( t \), temperature \( ϑ \), the stress states and environmental factors. As long as the maximum principal strain in a plastic part does not exceed this limit, the viscoelastic deformation of the plastic part will remain reversible [3]. On the other hand will exceeding this value result in damage of the material on the microscopic scale which will result in lasting deformation.

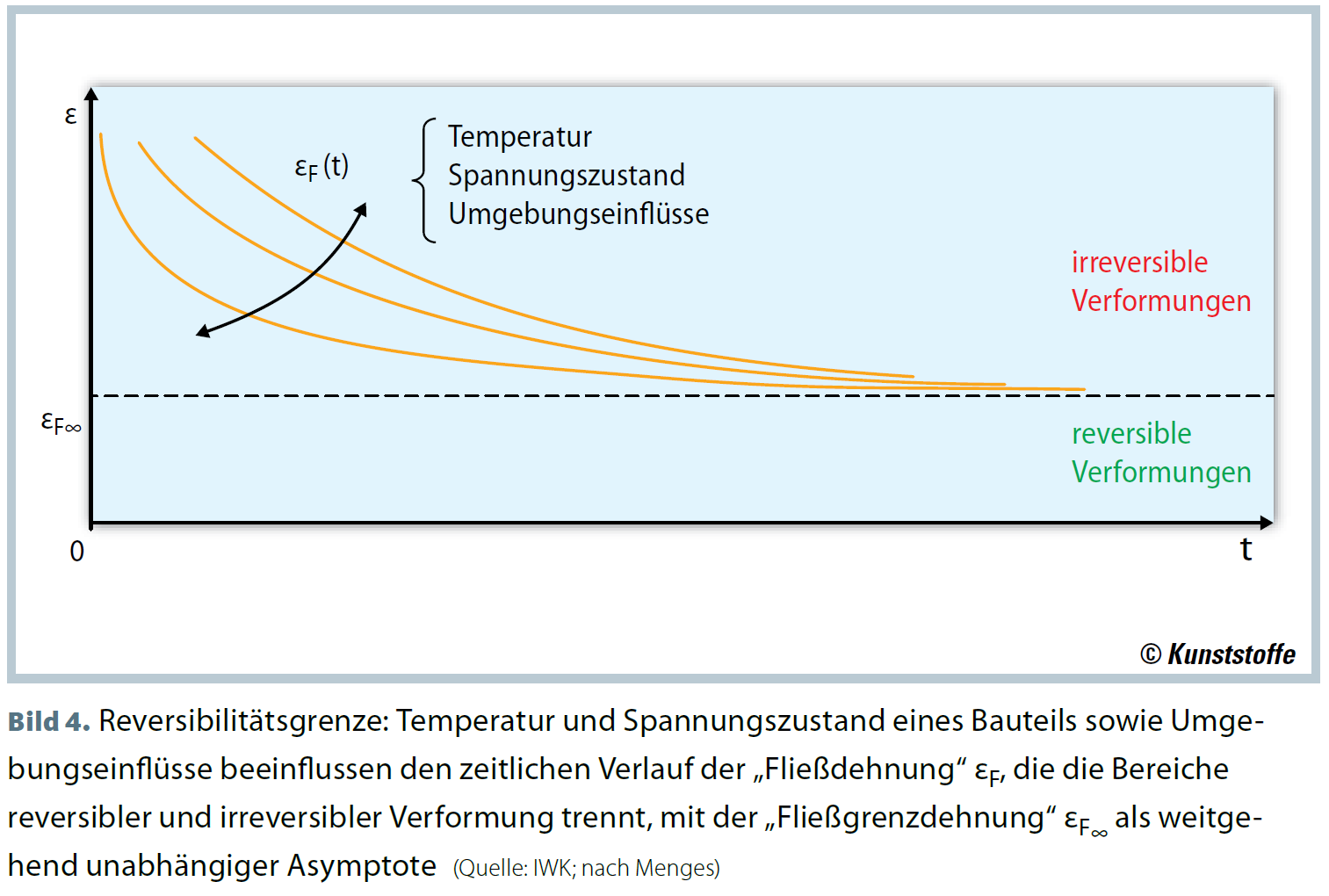
Figure 1: Reversibility strain \( ε_F (t) \) in dependence of time. Image taken from [3].

 

The image shows that the value of \(ε _F (t) \) approaches a constant value \(ε _{F∞} \) in the long term. This value is independent of load time, temperature, stress states, and environmental influences. Using this value as strain limit \(ε _G  = ε _{F∞} \)  therefore is a promising approach to simplify the design and evaluation of plastic parts, as it becomes independent of time, temperature and holds for static as well as cyclic loads [2].

Literature values of  \(ε _{F∞} \) exist for a variety of materials. Further, similar values can be used to describe whole families of materials, therefore allowing to assess the design of plastic parts even before the exact material and its supplier is known. Differences exist between amorphous and semi-crystalline plastics. For amorphous plastics, the value of \(ε _{F∞} = 0.8 \% \) can be used, with exception of PS, which only allows for \(ε _{F∞} = 0.4 \% \) [4]. The reversibility strain of semi-crystalline plastics can be estimated from their elastic modulus [4]:

\( ε_{F∞}≈5.0-3.1*(1-exp⁡(-0.9*\frac{E}{E_{ref}} ) ) \)

 

Where \( E_{ref} = 1000 \, MPa \)

 

Influencing factors

Influencing factors allow to consider different factors that will influence the value of the permissible strain. The factor \( C_1 \) is used to avoid overly conservative dimensioning, particularly when dealing with short-term loads at moderate temperatures. Other crucial factors in strain-based design include the influence of fiber or filler content and the impact of knit lines and weld seams, which can introduce weaknesses.

 

Influence of time & temperature \( C_1 \)

The material factor \( C_1 \) for the effect of time and temperature is an important consideration in strain-related design. For short-term loads at ambient temperatures we can get away with loading the material up to twice of the reversibility strain limit \(ε _{F∞} \) without risking damage [2]. The value of \( C_1 \) approaches 1 for increasing load durations and increasing temperature, underlying the previously made statement that the asymptotic limit of the reversibility strain is largely indifferent regarding time and temperature. By using an influencing factor  \( C_1 > 1 \) for short term loads under moderate temperatures we prevent being overly conservative in our design. The following table shows how \( C_1 \) can be estimated depending on temperature and duration of the load.

 

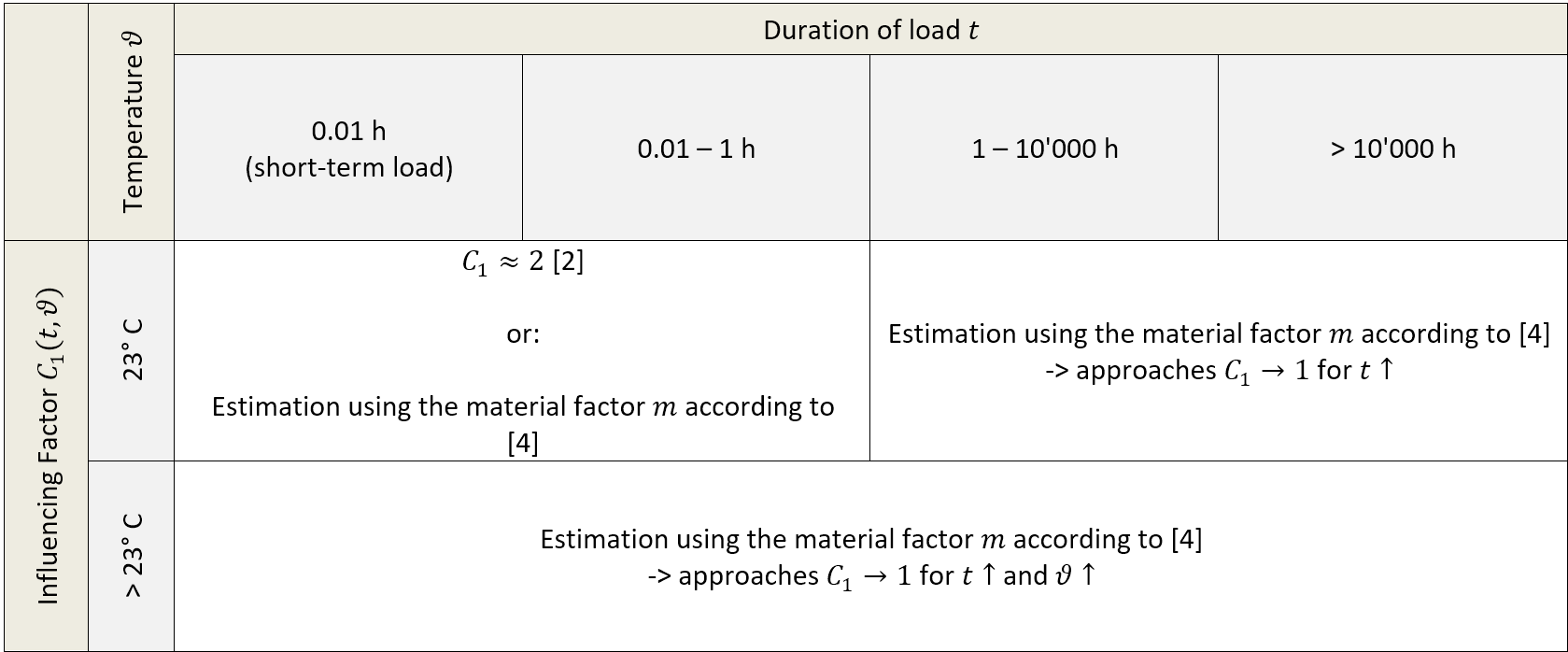
The material factor m is provided by [4] for various common materials (Table 2) and allows to calculate \( C_1 \) according to the following formulas:

\( C_1=1+0.8*m*f_{1t}*f_{1ϑ} \)

\(f_{1t}=exp⁡(-0.4*(2+log⁡(\frac{t}{t_0})))\)

\( f_{1ϑ}≈1.38-0.38*\frac{ϑ}{ϑ_R} \)

 

Where \(t_0 = 1 h\) and \(ϑ_R = 23°C \)

 

Material	Material factor \(m\)
PMMA	3.8
PVC	1.4
PC	4.8
POM	1.0
PP	2.3
Others	1.0

Table 2: Material factor \(m\) for different thermoplastic plastics taken from [4].

 

Influence of fiber and filler content \(C_2\)

Many plastic materials are infused with fibers to increase their stiffness and load bearing capacity. These fibers in turn reduce the allowable strain of the material, as they can promote damage within the material at reduced strain values. A rough estimation of the effect of fiber reinforcement on the permissible strain can be considered by using an influencing factor \( C_2≈0.5 \) as suggested by [2]. If the mass or volume fraction of the fibers is known, [4] and [5] provide analytical formulas to determine \(C_2\) .

 

Influence of knit lines \(C_3\)

Knit lines occur during the injection molding process of plastic parts in areas where molten material meets after being injected from different directions. These knit lines are often weak points in a design and should therefore be considered during development. If such knit lines cannot be prevented in critical areas of a design, their influence can be considered by an additional influencing factor \(C_3\). [4] suggest these values for amorphous and semi-crystalline materials:

Amorphous plastics: \( C_3≈0.45 ... 0.95\)

 

Semi-crystalline plastics: \( C_3≈0.85 ... 1.0\)

 

Influence of weld seams \(C_4\)

Like knit lines, weld seams can significantly influence the permissible strain. The influence can be estimated according to [4]:

\( C_4≈0.3 ... 0.8\)

 

Safety factor \(S\)

In many cases, a safety factor \(S=1\)  can be assumed, as damage in the micro range does not yet represent a dramatic failure and there is a large load reserve exceeding the yield point or fracture [2]. There is an exception if clouding of a transparent material must be avoided at all costs or if environmental media are present that favor stress cracking [2].

[4] suggest a safety value of \( S≈1.0 ... 1.2\) for unproblematic conditions and \( S≈1.2 ... 1.5\) critical cases. Of course, there are situations where even higher safety factors can be desired. As always, it is an important task of the designer to evaluate the given situation and find a practical value for these factors.

 

Evaluation of the maximum principal strain

Given the strain limit \(ε_G\), the influencing factors \(C_i\), and the safety factor \(S\), we are now able to evaluate the right-hand side of our initially defined deformation condition. This provides us with the permissible strain \(ε_{permissible}\) which the maximum principal strain in our design is not allowed to exceed:

 

\(ε_{max}=max(ε_1, ε_2, ε_3) ≤ ε_{permissible} = ε_G * \frac{C_1*C_2* ... * C_n}{S} \)

 

There exists some subgroup of problems for which strains can be calculated analytically. A noteworthy mention here are simple snap fits. [6] and [7] have developed analytical models for some simple yet common designs of snap fits for which maximum principal strains can be evaluated analytically.

 

For most more complex designs however, such analytical solutions are not feasible anymore. IMT therefore successfully utilizes advanced structural simulations, enabling the evaluation of complex designs and targeted design optimizations.

 

For such simulations, the material stiffness \(E_C\) needs to be known. In the case of plastic materials, the material stiffness is highly dependent on the temperature as well as the duration of the load. Plastics show a high tendency to creep, which is the material’s tendency to deform under sustained load over time. When it comes to material properties, values that have been determined experimentally are always the preferred option. However, such information is often unavailable for the chosen material, or the exact material might not yet be decided in early stages of the development process. In these cases, it is beneficial to have pragmatic approaches to estimate the needed quantities. Thankfully, academia has developed some easy-to-use approaches to estimate the material stiffness of plastic materials. The following table gives an overview of how material stiffness \(E_C\) can be determined for different temperatures and load times, depending on what material data is available.

 

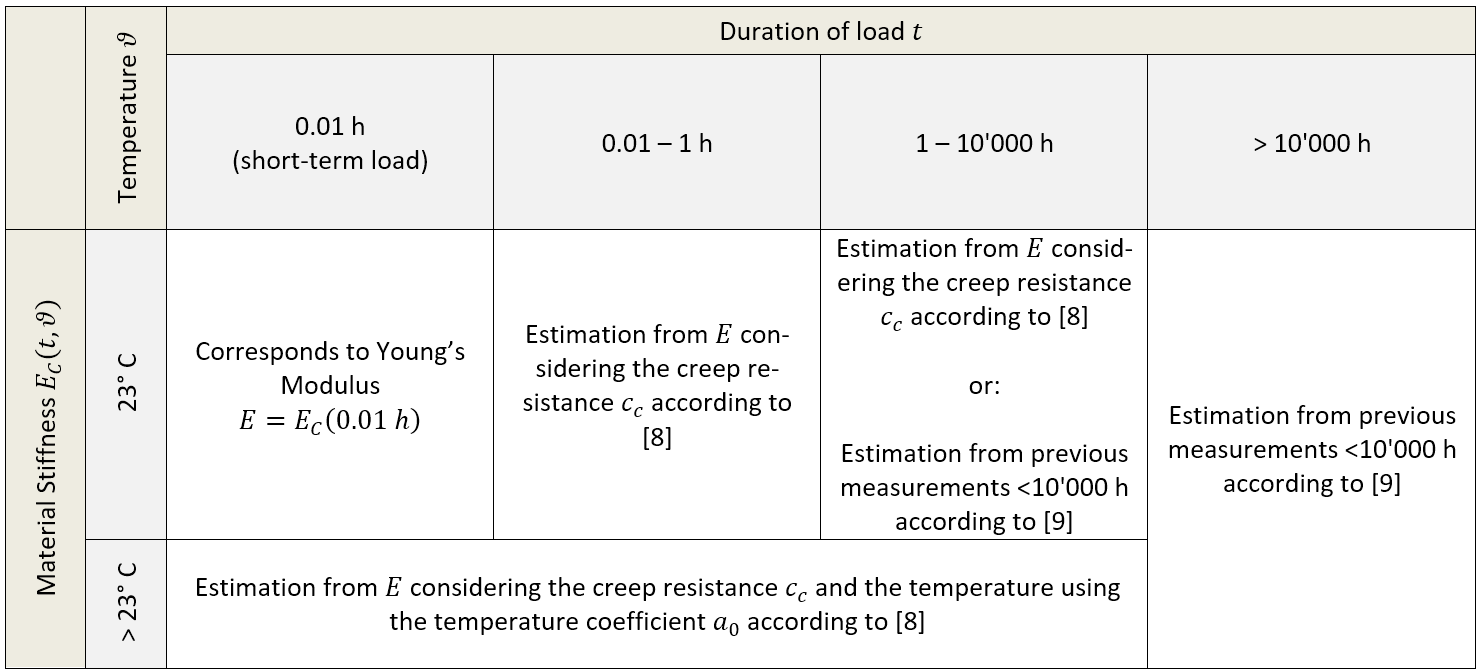
[8] provides the following formula to estimate the material stiffness \(E_C(t)\) depending on load duration from the Young’s Modulus \(E\) :

\( E_c (t)=E*\frac{3-(1-c_c )\,*\,log_{10}⁡ \,\frac{t}{t_0}}{3+2\,*\,(1-c_c)} \)

 

Where \( 10^{-2} \,h\,≤\,t\,≤10^4\,h \) is the duration of the load and \( t_0\,=\,1\,h\) is the reference time.

 

If additionally the influence of temperature \( ϑ \) must be considered, the material stiffness \( E_c \) can be modified according to [8]:

\( E_c(t,ϑ)\,=\,E_c(t,ϑ_0)\,*a_0^{(\frac{ϑ}{ϑ_0}-1)} \)

 

Where \( ϑ \, = \, 23° \,C \) is the reference temperature.

 

These formulas use the creep resistance \(c_C\) and the temperature coefficient \(a_0\) as defined by [8]. The following table provides values for some selected materials. More values can be found in the original publication [8].

 

Material	Creep resistance \(c_C\)	Temperature coefficient \(a_0\)	Temperature limit in °C
PC	0.88	0.85	120
PC+ABS	0.72
ABS	0.68	0.7	80
PS	0.80
PMMA	0.80
PE	0.45-0.6
PP	0.50
PA6 (dry)	0.73	0.45	60
POM	0.6-0.65	0.75	120

Table 4: Selection of creep resistance and temperature coefficients with corresponding temperature limit as taken from [8].

 

With these values, efficient simulation of plastic parts is possible, even taking the special behavior of plastics due to increased temperature and long-term load into account.

By evaluating the maximum principal strain in a design under load and making sure this value stays below the permissible strain, reversibility of the deformation can be ensured. This will result in robust and durable designs, withstanding even the most difficult environmental conditions.

 

Conclusion

IMT’s strain-based design methodology for plastic parts combines robust theoretical frameworks with practical tools. The design strategy is especially powerful in addressing the unique behavior of plastics under increased temperatures and long-term loads. The strain-based approach allows for early-stage design assessments using literature values and approximations, even when extensive material data is not yet available. By combining advanced simulation techniques and pragmatic estimation methods, IMT enhances product performance while maintaining development speed and cost-effectiveness.

 

References

[1]	A. Geyer, T. Röber and B. Christian, "Die kritische Dehnung nutzen," Kunststoffe, pp. 143-147, October 2017.
[2]	J. Kunz, "Ein Plädoyer für die dehnungsbezogene Auslegung," Kunststoffe, vol. 4, pp. 50-54, 2011.
[3]	J. Kunz, "Reversibilität als Auslegungskriterium," Kunststoffe, pp. 67-71, January 2018.
[4]	J. Kunz, "Dehngrenzen und sprödes Werkstoffverhalten," KunststoffXtra, 2022.
[5]	J. Küffer, "Eigenschaften, Werkstoffkennwerte, spezielle Verfahren," Konstruieren mit Kunststoffen, 2014.
[6]	J. Kunz, "Beiträge zu einer besseren Schnapphakenauslegung," SwissPlastics, November 2007.
[7]	IWK, "Gekröpfte Schnapphaken und ihre Auslegung," SwissPlastics, pp. 18-20, 2010.
[8]	J. Kunz, "Kriechmodul-Abschätzung und Kriechbeständigkeit," KunststoffXtra, pp. 23-26, March 2014.
[9]	K. Faust, "Berechnen statt voraussagen," Kunststoffe, pp. 80-85, April 2022.